An introduction to statistics in R
A series of tutorials by Mark Peterson for working in R
Chapter Navigation
- Basics of Data in R
- Plotting and evaluating one categorical variable
- Plotting and evaluating two categorical variables
- Analyzing shape and center of one quantitative variable
- Analyzing the spread of one quantitative variable
- Relationships between quantitative and categorical data
- Relationships between two quantitative variables
- Final Thoughts on linear regression
- A bit off topic - functions, grep, and colors
- Sampling and Loops
- Confidence Intervals
- Bootstrapping
- More on Bootstrapping
- Hypothesis testing and p-values
- Differences in proportions and statistical thresholds
- Hypothesis testing for means
- Final thoughts on hypothesis testing
- Approximating with a distribution model
- Using the normal model in practice
- Approximating for a single proportion
- Null distribution for a single proportion and limitations
- Approximating for a single mean
- CI and hypothesis tests for a single mean
- Approximating a difference in proportions
- Hypothesis test for a difference in proportions
- Difference in means
- Difference in means - Hypothesis testing and paired differences
- Shortcuts
- Testing categorical variables with Chi-sqare
- Testing proportions in groups
- Comparing the means of many groups
- Linear Regression
- Multiple Regression
- Basic Probability
- Random variables
- Conditional Probability
- Bayesian Analysis
Relationships between quantitative and categorical data
6.1 Load today’s data
Start by loading today’s data. If you need to download the data, you can do so from these links, Save each to your data directory, and you should be set.
- hotdogs.csv
- Data on nutritional information for various types of hotdogs
- fastPlant.csv
- Growth data on plants under various treatments (High vs. Low light and fertilizer) Grown by students at Juniata College in the fall of 2013.
- Pizza_Prices.csv
- Gives information on weekly pizza sales (number of slices sold and average price) for various cities.
# Set working directory
# Note: copy the path from your old script to match your directories
setwd("~/path/to/class/scripts")
# Load data
hotdogs <- read.csv("../data/hotdogs.csv")
fastPlant <- read.csv("../data/fastPlant.csv")
pizza <- read.csv("../data/Pizza_Prices.csv")6.2 Overview
Broad, general descriptions of data, like we have done in previous chapters, is a great way to get a sense of the data. However, we must then consider: so what?
What does it meant that the median number of pizza slices sold per week in Denver is 43,158? Is that a lot? How can we know?
The only way to understand the context of these summaries is in relation to other variables. Sometimes we have an intuitive sense of these (e.g., you would know the price of pizza was high if the mean we $16/slice). Often, however, we need to directly compare it to something else. In this chapter, we will compare different variables using a few different methods. In later chapters, we will start trying to interpret these differences.
6.3 Compare values in different columns
6.3.1 Numeric comparison
The simplest use case is when we have completely separate columns with data. So, let’s start by asking about differences in the price of pizza in Denver and Dallas. Well, we’d probably like to see the mean, the median, and some information about the spread for the price in each city. What function gave us those values?
.
.
.
.
.
Yep: summary() gives us that information. So, we can run summary() on each column and compare the values.
# Run summary on each column
# Format beautified, but the numbers are the same as you'll get
summary(pizza$DEN.Price)
summary(pizza$DAL.Price)| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|
| DEN | 2.11 | 2.458 | 2.56 | 2.566 | 2.70 | 2.99 |
| DAL | 2.21 | 2.510 | 2.61 | 2.619 | 2.72 | 3.05 |
So, we can, relatively quickly, see that the distributions are really, really similar. Both measures of the center are very close, and ther spreads are quite similar as well. In this case, if we were only interested in the mean, we could have just run mean() on each column instead.
Now, this works great for two columns. However, if we want to look at more than two columns, say, adding in the price of pizza in Baltimore, it gets to be a lot of lines of typing. Luckily, there is a bit of a shortcut for summary.
First, we could use apply() over the columns of interest, just like we did for categorical variables. Let’s say we want the mean of every column from pizza:
# Use apply to get all the means
apply(pizza, 2, mean)## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Warning in mean.default(newX[, i], ...): argument is not numeric or
## logical: returning NA## Week BAL.Sales.vol BAL.Price DAL.Sales.vol DAL.Price
## NA NA NA NA NA
## CHI.Sales.vol CHI.Price DEN.Sales.vol DEN.Price
## NA NA NA NAOops – that gave us a bunch of warnings. Is there something wrong with one of our columns. Well, the Week column isn’t numbers, so mean() doesn’t know what to do with it[*] The reason they all become NA instead of just week is that apply() converts the entire data.frame to a matrix before calculating anything. Because Week is non-numeric, it makes the entire matrix non-numeric, thus propogating the error to all columns. . We can tell R to ignore that column in a few ways. The simplest is by using the - operator. As we saw in the first chapter, we can select columns from a data.frame using the [ row , col ] options. Putting a minus sign (-) in front of a number tells R: “Give me everything except this column (or row).” So, let’s try it here:
# Use apply to get all the means
apply(pizza[,-1], 2, mean)## BAL.Sales.vol BAL.Price DAL.Sales.vol DAL.Price CHI.Sales.vol
## 2.710003e+04 2.847179e+00 5.173844e+04 2.619038e+00 2.275120e+05
## CHI.Price DEN.Sales.vol DEN.Price
## 2.616731e+00 4.574289e+04 2.566026e+00That looks a lot better. However, the numbers are still in scientific notation because the sales volumes are so large. Let’s try it with just the Price columns. Here, instead of giving R column numbers, we can give it column names. Note that they must be inside quotation marks (single or double) and that if you have more than one, they all need to be inside of c().
# Get just the Prices we wanted
apply(pizza[,c("DAL.Price","BAL.Price","DEN.Price")], 2, mean)## DAL.Price BAL.Price DEN.Price
## 2.619038 2.847179 2.566026Even better. Now we can quicly see that the mean price per slice of pizza is a bit higher in Baltimore than the other cities. Now, let’s look at the summary() of those columns to see if the spread backs that up. All we need to do is change mean to summary at the end of the function. Copy the line calculating the means and make that change. You should get something that looks like this (my formatting cleaned for the web).
| DAL.Price | BAL.Price | DEN.Price | |
|---|---|---|---|
| Min. | 2.210 | 2.050 | 2.110 |
| 1st Qu. | 2.510 | 2.685 | 2.458 |
| Median | 2.610 | 2.865 | 2.560 |
| Mean | 2.619 | 2.847 | 2.566 |
| 3rd Qu. | 2.720 | 3.040 | 2.700 |
| Max. | 3.050 | 3.400 | 2.990 |
Here, we see that, while the minimum price is similar, the price at all of the other points of interest in the spread is higher in Baltimore.
As one last point, summary has an additional nice feature in that it is designed to work well on data.frames (as well as lots of other data types). Specifically, if you run summary() on a data.frame, it will give you a sensible summary of each column. This can be a great way to get a broad overview of your data, and is one of the functions I almost always run when I open a new dataset.
# Run summary on the whole data.frame
summary(pizza)## Week BAL.Sales.vol BAL.Price
## 10/1/1994 : 1 Min. : 12743 Min. :2.050
## 10/12/1996: 1 1st Qu.: 19102 1st Qu.:2.685
## 10/14/1995: 1 Median : 22588 Median :2.865
## 10/15/1994: 1 Mean : 27100 Mean :2.847
## 10/19/1996: 1 3rd Qu.: 30050 3rd Qu.:3.040
## 10/21/1995: 1 Max. :101915 Max. :3.400
## (Other) :150
## DAL.Sales.vol DAL.Price CHI.Sales.vol
## Min. :35426 Min. :2.210 Min. :114110
## 1st Qu.:45626 1st Qu.:2.510 1st Qu.:180715
## Median :49864 Median :2.610 Median :208986
## Mean :51738 Mean :2.619 Mean :227512
## 3rd Qu.:56472 3rd Qu.:2.720 3rd Qu.:252626
## Max. :85282 Max. :3.050 Max. :788517
##
## CHI.Price DEN.Sales.vol DEN.Price
## Min. :1.550 Min. :27328 Min. :2.110
## 1st Qu.:2.527 1st Qu.:37658 1st Qu.:2.458
## Median :2.650 Median :43158 Median :2.560
## Mean :2.617 Mean :45743 Mean :2.566
## 3rd Qu.:2.740 3rd Qu.:50210 3rd Qu.:2.700
## Max. :3.030 Max. :95414 Max. :2.990
## Note that it automatically detects the column type and gives you useful information about it.
6.3.2 Boxplots
Now, numerical information is great, and is vital to making any point you need to about data. However, a picture is worth (at least) 1000 words, and is a necessary component of any data presentation (paper, talk, report, etc.). A simple way to show the difference or similarity between two variables is with a boxplot. The function boxplot() works very similarly for multiple variables, and (like we saw above) there are several ways to use it.
The most straightforward way is to just give it multiple columns that we were interested in. So, as above, let’s start by comparing the price of pizza in Baltimore, Dallas and Denver.
# Make a boxplot of the prices
boxplot(pizza$BAL.Price, pizza$DEN.Price, pizza$DAL.Price)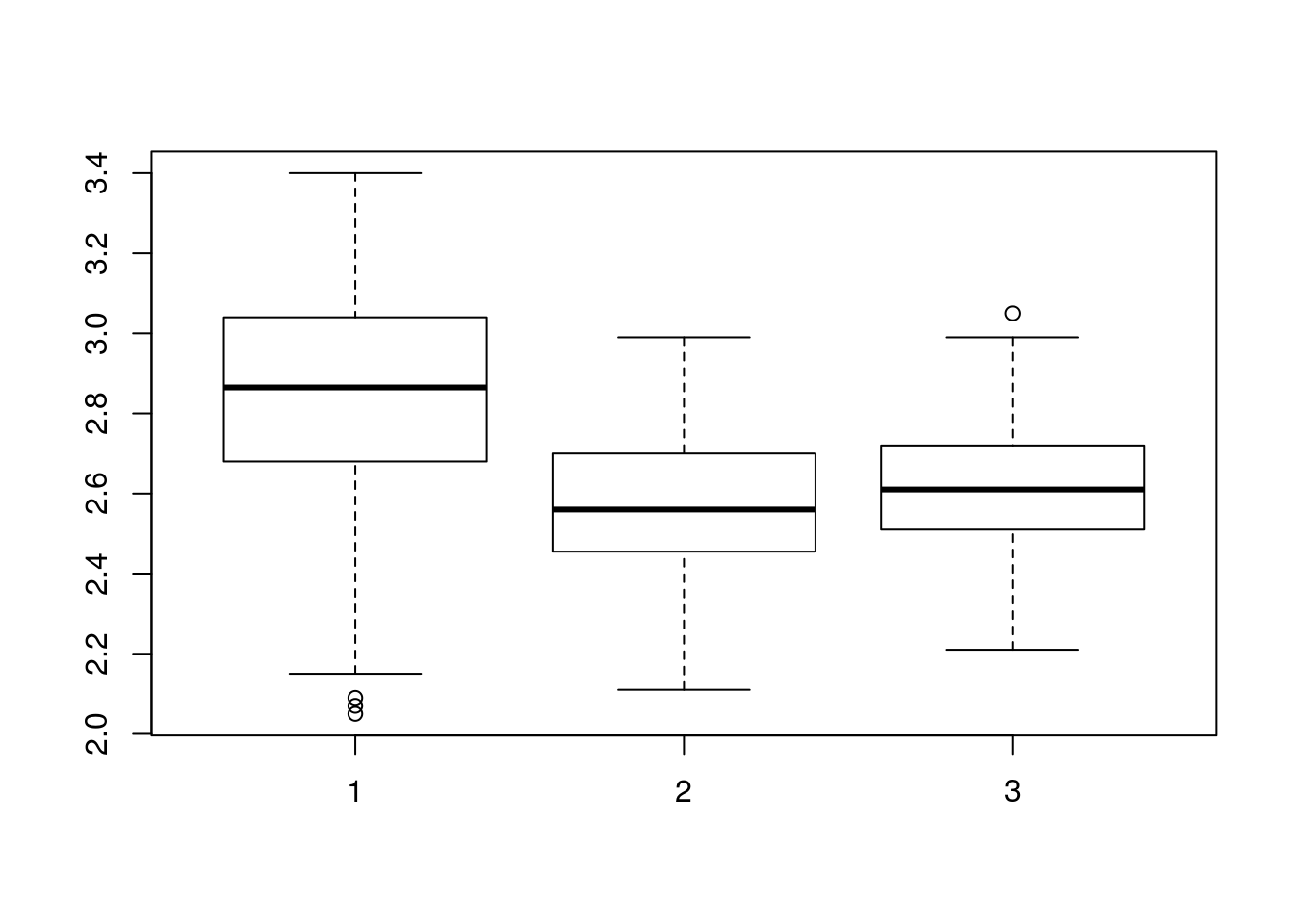
Notice that, instead of city names, we see the numbers 1, 2, and 3 along the bottom. This is a consequence of how boxplot() handles its inputs, but is obviosly not acceptable for a final plot. Luckily, we can set the names with the simple addition of the names = argument. Pass in the labels you want to use for each (e.g., the names of the cities) in the same order as the columns you give to boxplot() (so they match up). Try it here, and make sure to add axis and plot labels as we have before.
# Add labels to the plot
boxplot(pizza$BAL.Price, pizza$DEN.Price, pizza$DAL.Price,
names = c("Baltimore","Denver","Dallas"))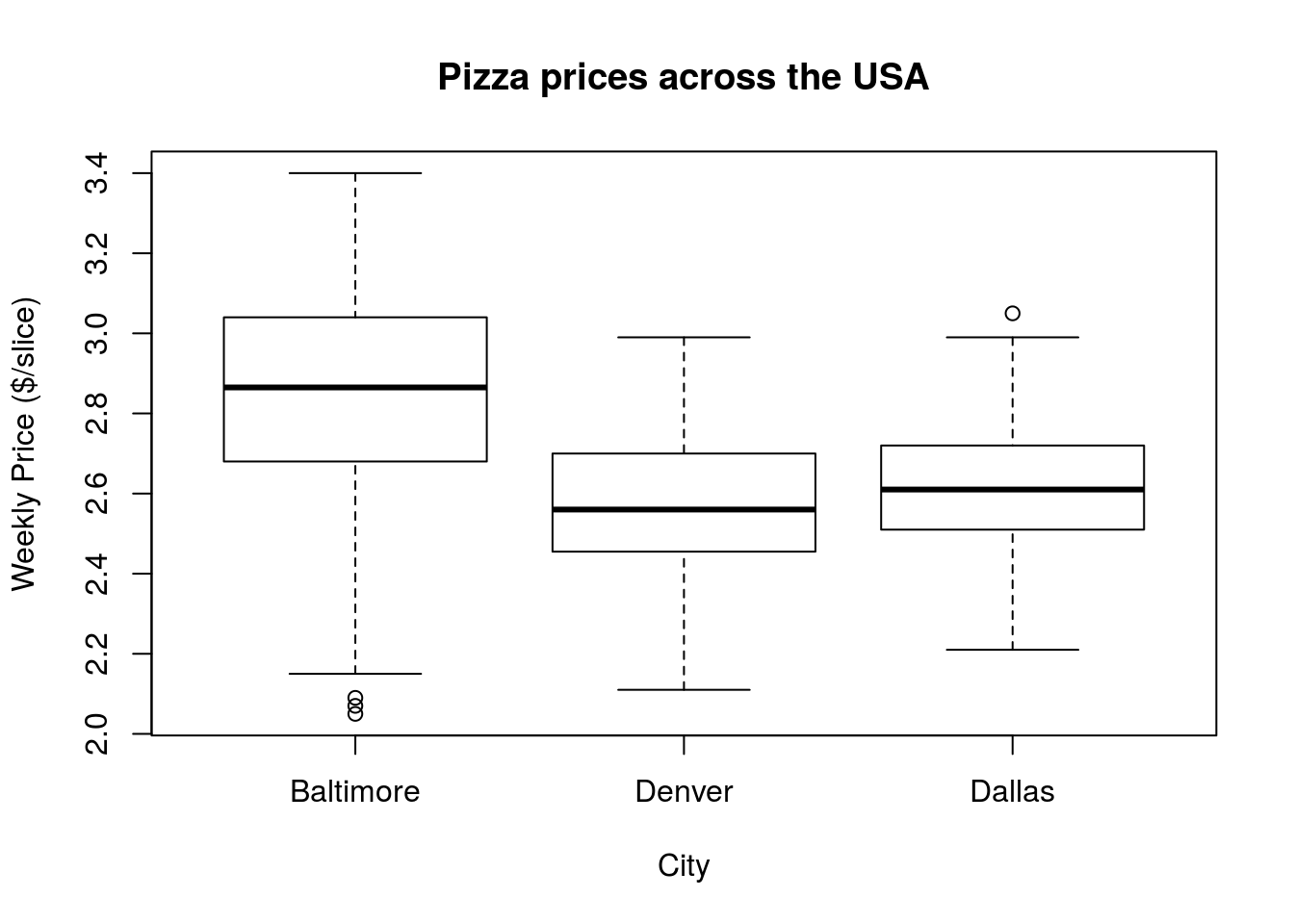
From this visualization, it is very clear that pizza is a lot more expensive in Baltimore than in either Denver or Dallas, though the latter two cities look pretty similar.
Finally, we can also see how boxplot() works if we pass in the data as a data.frame (limited to the columns we want). Now, instead of typing each as a separate vector, we just name the columns in the [] selector as we did above. Try it first with no arguments:
# Make boxplot with data.fram
boxplot(pizza[, c("BAL.Price", "DEN.Price", "DAL.Price")] )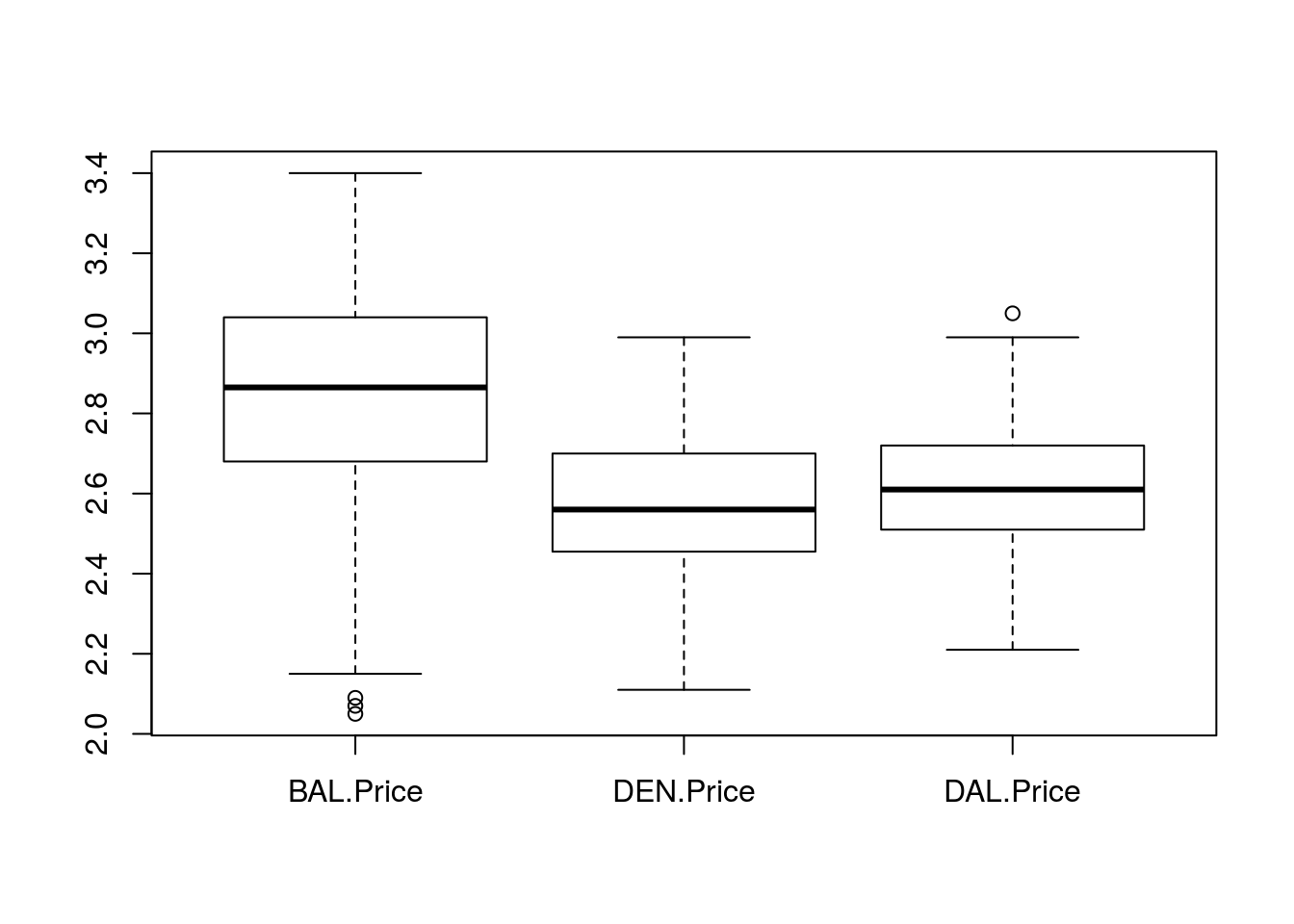
Note that R now uses the column names as the labels. If your column names are nicely formatted, that might be sufficient. However, you can still use the names = argument to override the defaults (if, for example, you don’t want the “.Price” part on the plot). In general, it is always a good idea to make a plot first, then add labels – just in case it comes out differently than you expect.
6.3.3 Histograms
Now, to look at the distributions more closely, we may want to make histograms. Because the variables are in separate columns, we make these exactly the same way we would make them for single variables.
However, we also want them to show up on the same plot. For that, we start our introduction to using the function par() to set the graphical parameters for output plots. There are a lot of options that can be set with par() (see ?par for details), but we will start with just setting how many figures to put on a plot. One word of warning: the easiest way to undo parameters that you don’t like it to clear the plots, which resets to the defaults (in RStudio, you can click on the broom icon that says “Clear All” in the plot window to do this).
The parameter we want to set is the layout of the plot, which can be set with par( mfrow = c(nr, nc) ) where nr is the number of rows we want and nc is the number of columns[*] This can also be set with mfcol = (nr, nc) to similar effect. The difference is the order in which the plots are filled. Setting mfrow means that the plots will be made in rows, mfcol means they will be filled in columns. For our example, and most we use, this distinction won’t be important, and mfrow is slightly more often the intuitive choice. . Here, we probably want two rows and one column.
Note that, especially if your RStudio screen is small to be reading these notes, you may get a “Plot margins too large” warning. If you do, make the plot window bigger try making the plot window bigger.
In addition, note that I reset the mfrow parameter to its default so that our next plot won’t be stuck on half of the plot window. this is generally a really good idea.
# set the parameters
par( mfrow = c(2,1))
# Make the histograms
hist(pizza$BAL.Price)
hist(pizza$DEN.Price)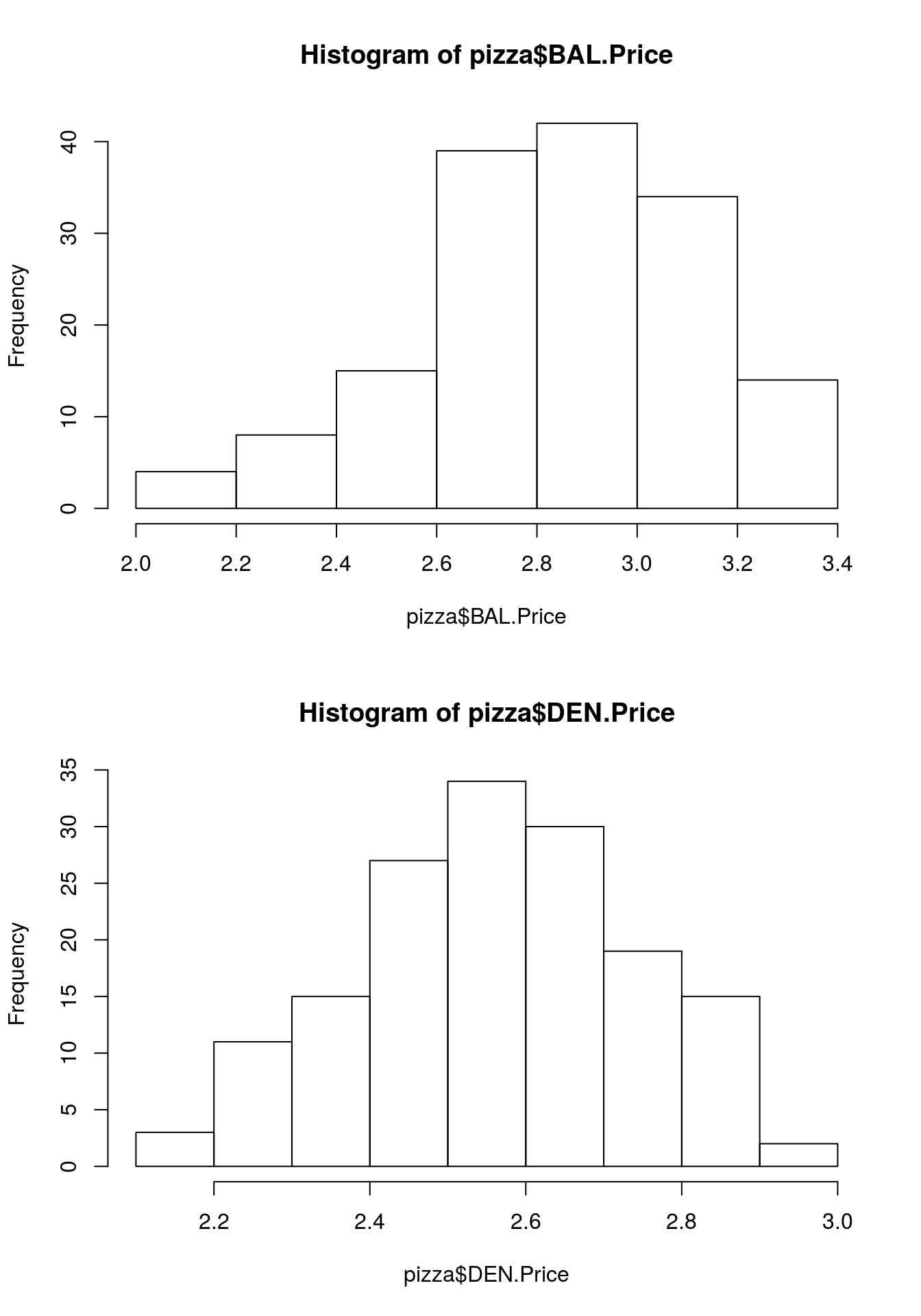
# Reset so we don't keep putting two plots on each thing.
par( mfrow = c(1,1))Now that the mechanics are out of the way, let’s inspect the plots. At first glance, it may appear that, unlike in the boxplots, the price of pizza in Baltimore seems pretty similar to that in Denver. But: look closer at the axis. Notice that they x-axis on the two plots is very different. This is one of the most common problems with data presentation (both by accident and by people actively trying to mis-represent data).
To put these on the same scale, we will use the argument xlim = in our call to hist(). This sets the extremes of the plot area, so it lets us put both plots on the same axis. Go back to your lines creating the histograms, and make them look like this:
# set the parameters
par( mfrow = c(2,1))
# Make the histograms
hist(pizza$BAL.Price, xlim = c(2, 3.4))
hist(pizza$DEN.Price, xlim = c(2, 3.4))
# Reset so we don't keep putting two plots on each thing.
par( mfrow = c(1,1))Then, add axis and title labels to finalize the plots:
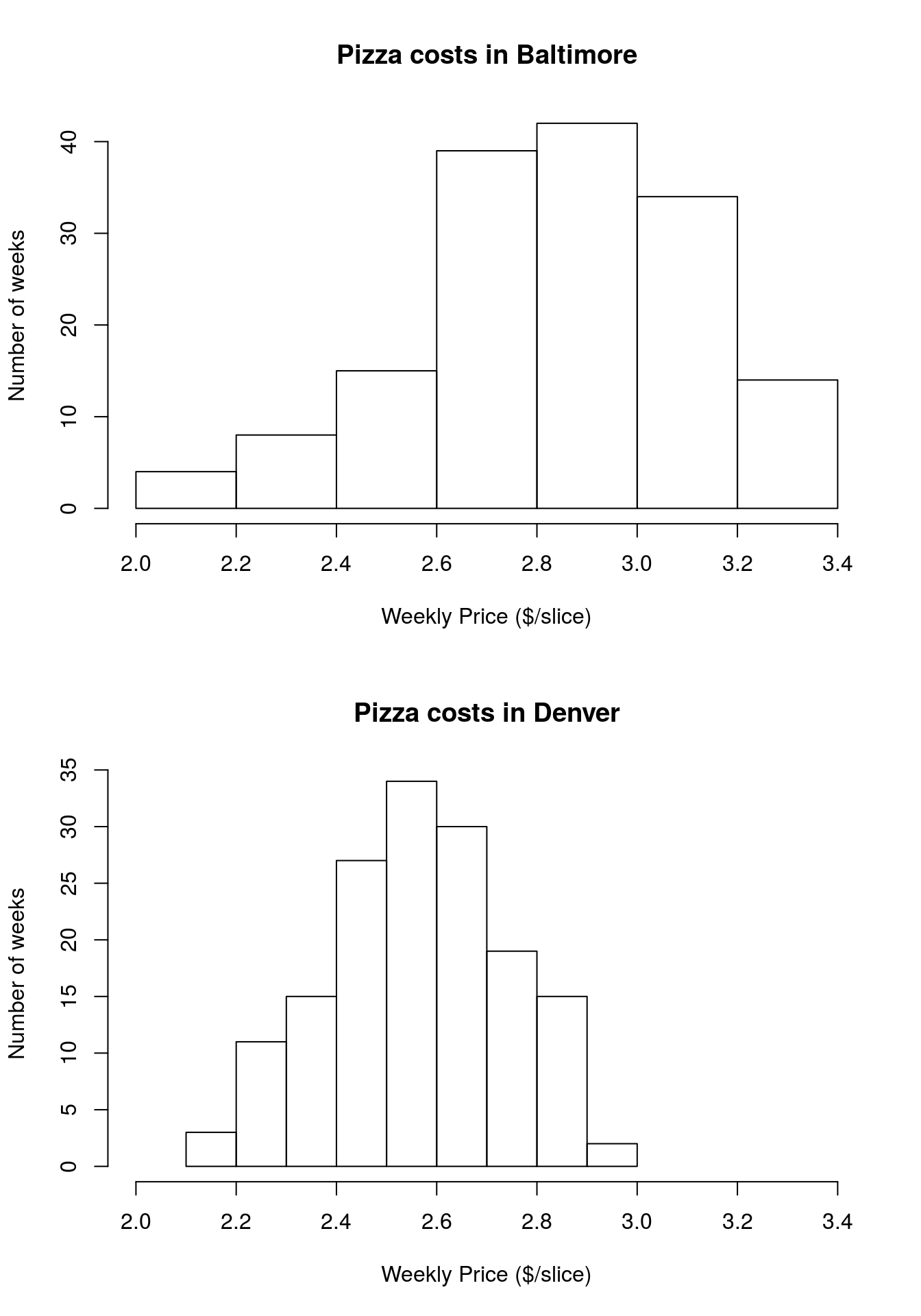
Now, like in the box plots, it is much more clear how the costs differ in the two cities.
6.4 Try it out (I)
Now, try it out for yourself by comparing the sales volume of pizza in Denver and Chicago (columns DEN.Sales.vol and CHI.Sales.vol). Report numerical summary and make both a boxplot and histogram comparing the two cities, then interpret your findings in a comment. Your plots outputs should look something like this:
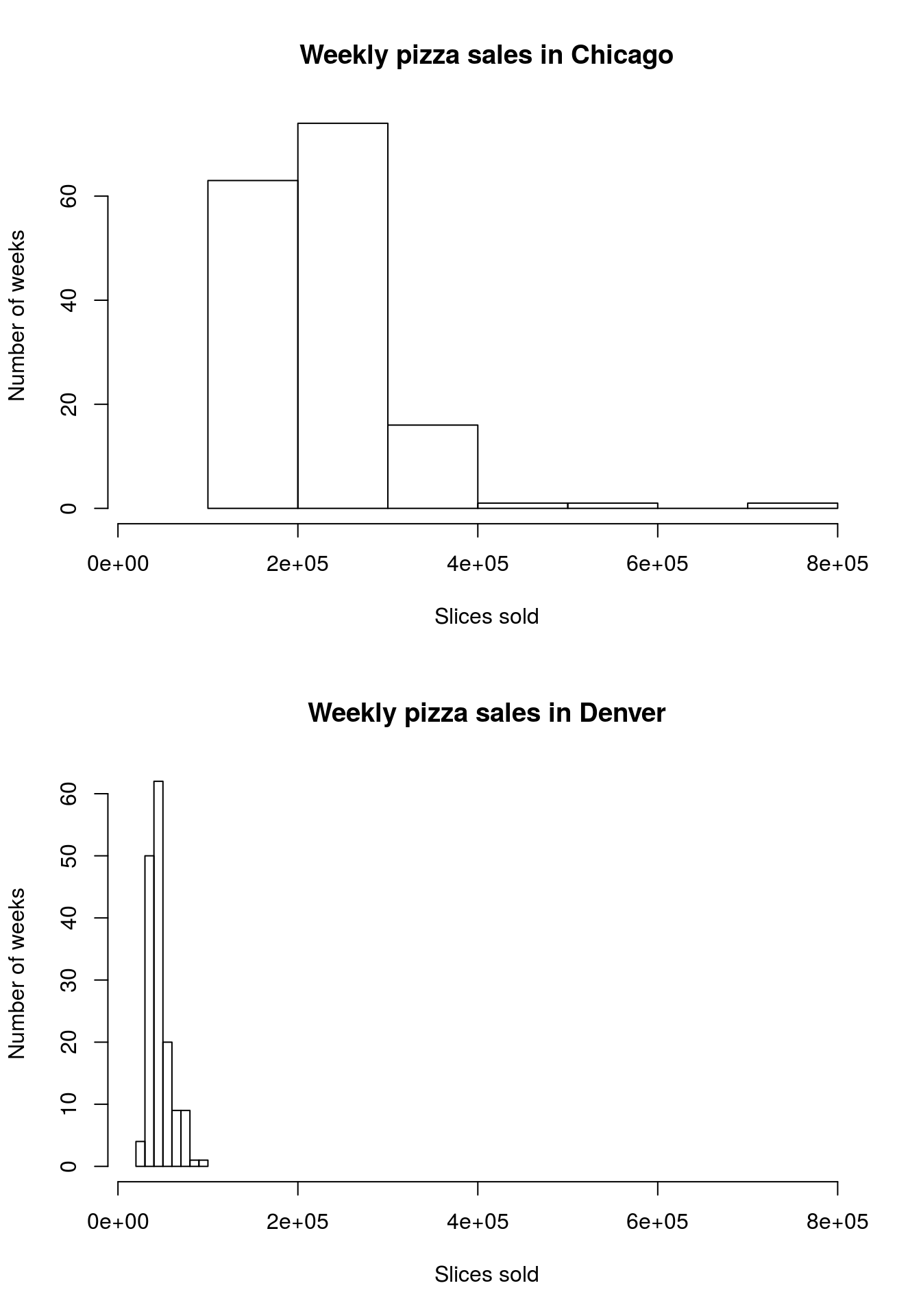
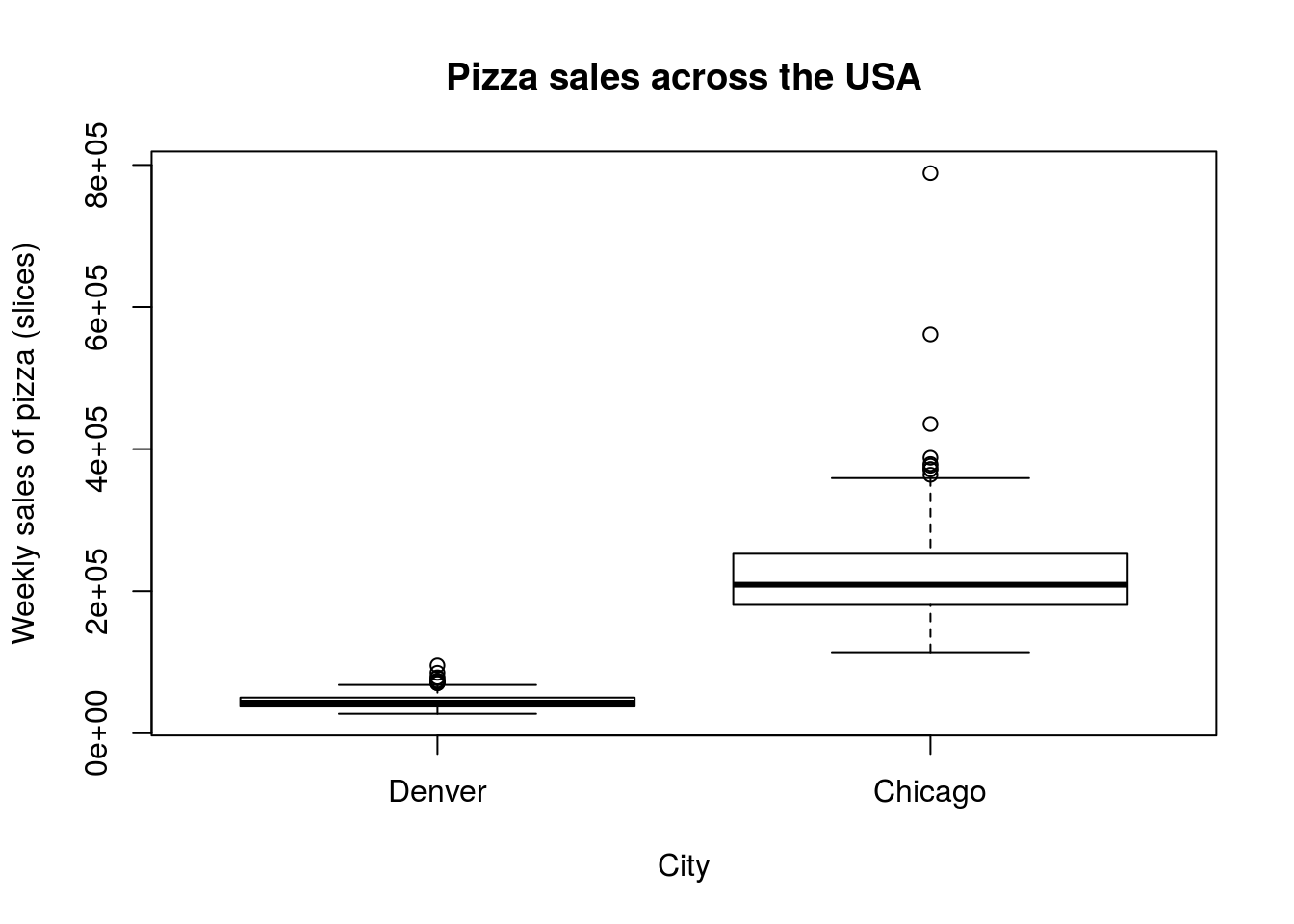
| DEN.Sales.vol | CHI.Sales.vol | |
|---|---|---|
| Min. | 27330 | 114100 |
| 1st Qu. | 37660 | 180700 |
| Median | 43160 | 209000 |
| Mean | 45740 | 227500 |
| 3rd Qu. | 50210 | 252600 |
| Max. | 95410 | 788500 |
6.5 Compare values in the same column
The above work great when we have data in separate columns. However, most data files will have all similar values in a single column. For example lets use head to look at the hotdogs data:
# Look at hotdogs data
head(hotdogs)| Type | Calories | Sodium |
|---|---|---|
| Beef | 186 | 495 |
| Beef | 181 | 477 |
| Beef | 176 | 425 |
| Beef | 149 | 322 |
| Beef | 184 | 482 |
| Beef | 190 | 587 |
We can also use summary() to get a peek at all of the data:
# Look at hotdogs data
summary(hotdogs)## Type Calories Sodium
## Beef :20 Min. : 86.0 Min. :144.0
## Meat :17 1st Qu.:132.0 1st Qu.:362.5
## Poultry:17 Median :145.0 Median :405.0
## Mean :145.4 Mean :424.8
## 3rd Qu.:172.8 3rd Qu.:503.5
## Max. :195.0 Max. :645.0Here, there is only one column for Calories and one for Sodium. We could use the outputs here to compare calories to sodium, but that doesn’t make much sense to do. More likely, we want to know something like if the Calories differ between types of hotdogs. So we will need a different approach.
6.5.1 Direct numerical calculations
The first solution is to just turn our columns into separate vectors. We can do this using the [ ] selection method on the column. Note that, when we are working with a sinlge vector (like a column) we only need on value to access the values (because there are not two dimensions). Because we are “indexing” with another variable (in this case, the hotdog type), we can ask to only be shown places where it matches. Here is a simple example showing that for a numeric variable:
# Create a test variable
test <- c(1, 1, 2, 3)
test## [1] 1 1 2 3# See where the value is "1"
test == 1## [1] TRUE TRUE FALSE FALSE# Show the values where test is "1"
test[test == 1]## [1] 1 1As you can see, the double equal sign == is used to ask “does this variable equal this other value?” When we put it inside of square brackets ([ ]), R returns the value for each place where the expression is TRUE.
Now, let’s use that on the hotdog data. Let’s first show the calorie values for all of the “Meat” hotdogs (generic meat, not specifically limited to one type).
# Show the Meat hotdog calories
hotdogs$Calories[ hotdogs$Type == "Meat"]## [1] 173 191 182 190 172 147 146 139 175 136 179 153 107 195 135 140 138Now, instead of 54 enteries, we only get 17 enteries. We can use this method to get summary information about each separately. So, if we want to know the mean of each type, we just run:
# Calculate mean calories of each type
mean(hotdogs$Calories[ hotdogs$Type == "Beef"])
mean(hotdogs$Calories[ hotdogs$Type == "Meat"])
mean(hotdogs$Calories[ hotdogs$Type == "Poultry"])From this, it is clear that the mean for Poultry hotdogs is lower than for the other types, but we probably want to know something about the spread too. If we want to see the full numeric summary, we just replace the mean with summary and can see all of those enteries. To do this, I just copied the above lines, pasted them below, then changed that one word.
# Calculate mean calories of each type
summary(hotdogs$Calories[ hotdogs$Type == "Beef"])
summary(hotdogs$Calories[ hotdogs$Type == "Meat"])
summary(hotdogs$Calories[ hotdogs$Type == "Poultry"])Looking at the values it is clear that Poultry hotdogs look substantially different in Calories than do Beef or Meat hotdogs. In a later we will anlyze that difference more formally.
6.5.2 A shortcut
Even for three types, it is clear that this approach takes a lot of typing, which can lead to typos. It is still often the best approach, especially if we need to save something about the values (more on that coming in a future chapter). However, especially if we just want a quick look at the data, there are several shortcuts (I’ve used at least four methods to do this). The simplest is to use the function by() which takes a set of data (such as a vector), splits it by another one, then computes a function on each portion. This works a lot like apply() in that we can either give it a single named function or right our own. For now, we will stick with named functions, but remember that the other option exists.
# Use by to calculat summaries
by(hotdogs$Calories, hotdogs$Type, summary)## hotdogs$Type: Beef
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 111.0 140.5 152.5 156.8 177.2 190.0
## --------------------------------------------------------
## hotdogs$Type: Meat
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 107.0 139.0 153.0 158.7 179.0 195.0
## --------------------------------------------------------
## hotdogs$Type: Poultry
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 86.0 102.0 113.0 118.8 142.0 152.0This way, there is no worrying about typos of the Types of hotdogs, and everything is printed neatly for us. Replacing summary with mean will return just the mean for each, or we could write our own function. the output will always be split by those ---- lines, to make visualization easy.
6.5.3 Boxplots
Now that we have the five-number summaries, let’s plot them. Here we will see a new feature of plot(): the ability to use a formula. In R, many (and I mean many) functions allow us to specify what we want to do using a formula. All formulas look something like:
A ~ B
Note that is a tilde (~) between those letters. It is usually in the top left of the keyboard and requires you to hit shift to type it. Think of like: “plot A by B”. For factors (like the Type of hotdog), R automatically creates a boxplot for us. (You can call boxplot directly, but it uses slightly different defaults that I don’t like as well.) Let’s see it in action:
# Make a simple boxplot of calories by type
plot(hotdogs$Calories ~ hotdogs$Type)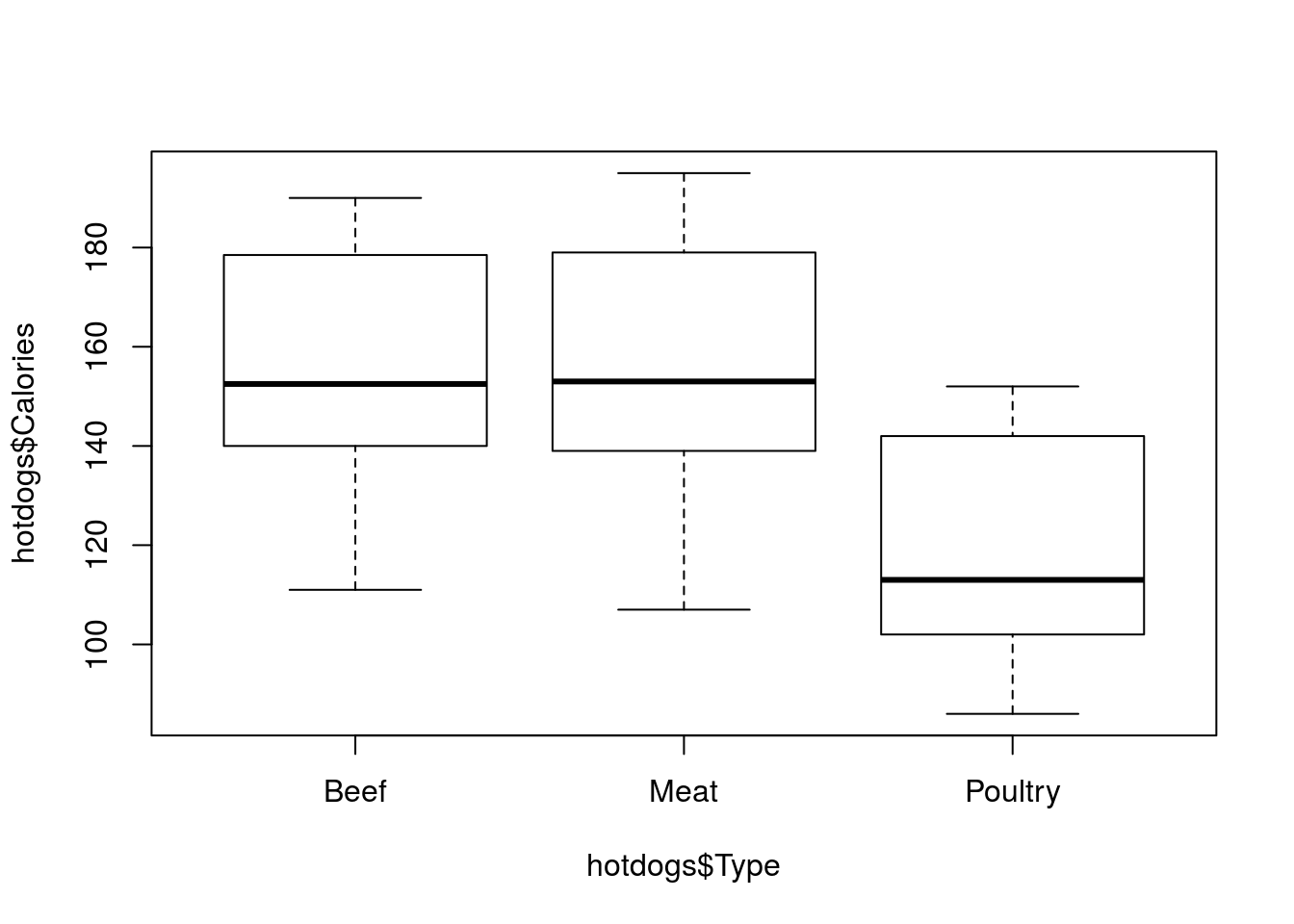
And bam! We can quickly visualize the difference between the Types. As we saw from the numerical summaries, Poultry hotdogs appear to have much lower caloric levels. But, two things bug me about this plot. First, typing hotdogs$ twice was obnoxious and makes the line of code longer. Second, I really don’t want hotdogs$ showing up on the plot. Luckily, both can be solved in the same way: the use of the data = argument. This allows us to specify a data.frame from which to pull our other information, then we only need to type the column names (and R knows to look for them).
# Use the data = argument
plot(Calories ~ Type, data = hotdogs)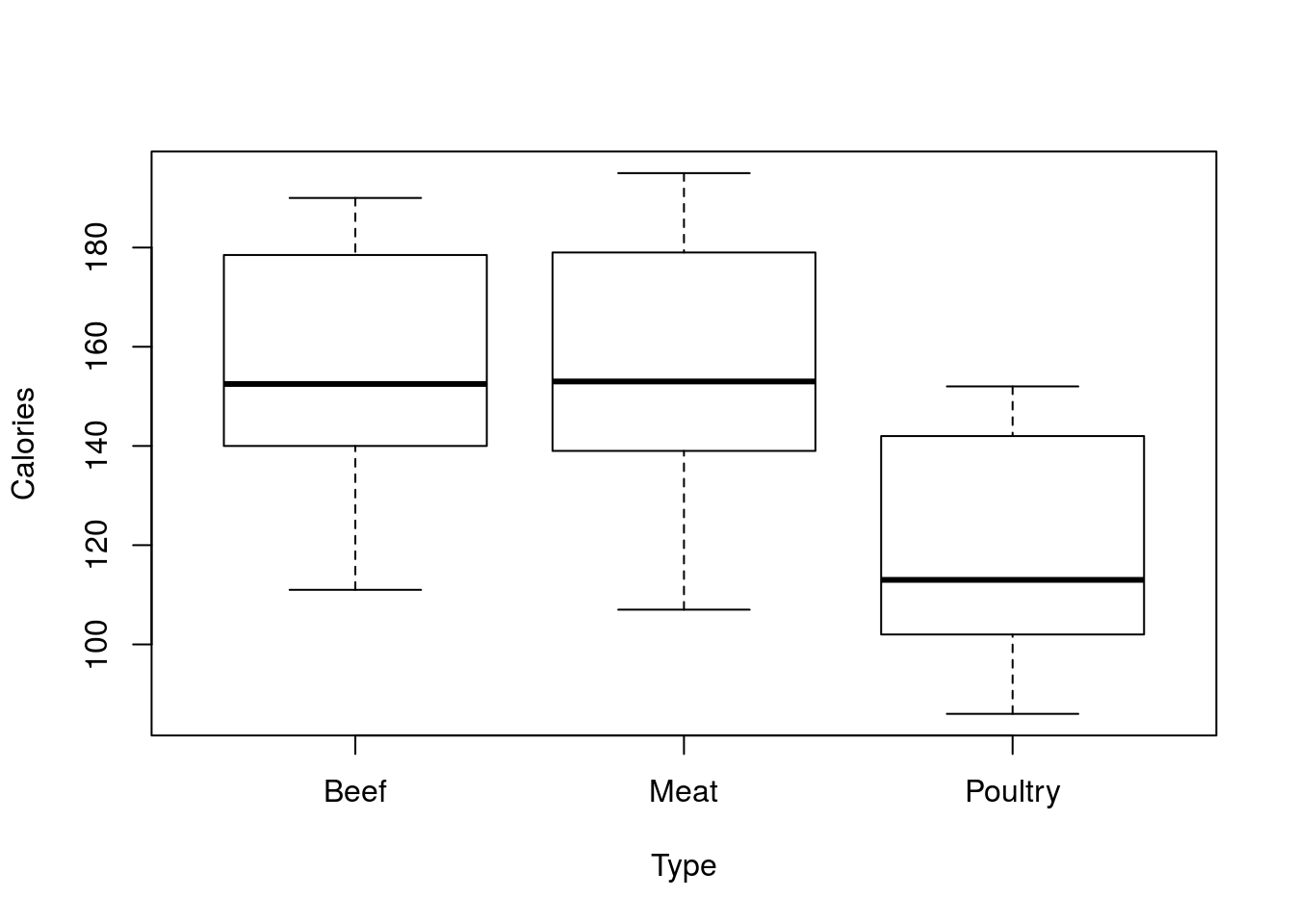
Now, it may seem that this is just a simple hack to change the labels and make the code look nicer. It does both of those things, but it also does so much more. For this plot, one thing it makes easy is selecting a subset of the data. Let’s say we no longer care about Poultry hotdogs. By setting the data to exclude those rows, we can limit what is plotted (without this, we’d need to put the same limit on both inputs). To accomplish this, we will use the != logical test, which is computer for “does not equal.” Because we are selecting rows, we want to put it before the comma inside our square brackets.
# Select a subset
plot(Calories ~ Type, data = hotdogs[hotdogs$Type != "Poultry", ])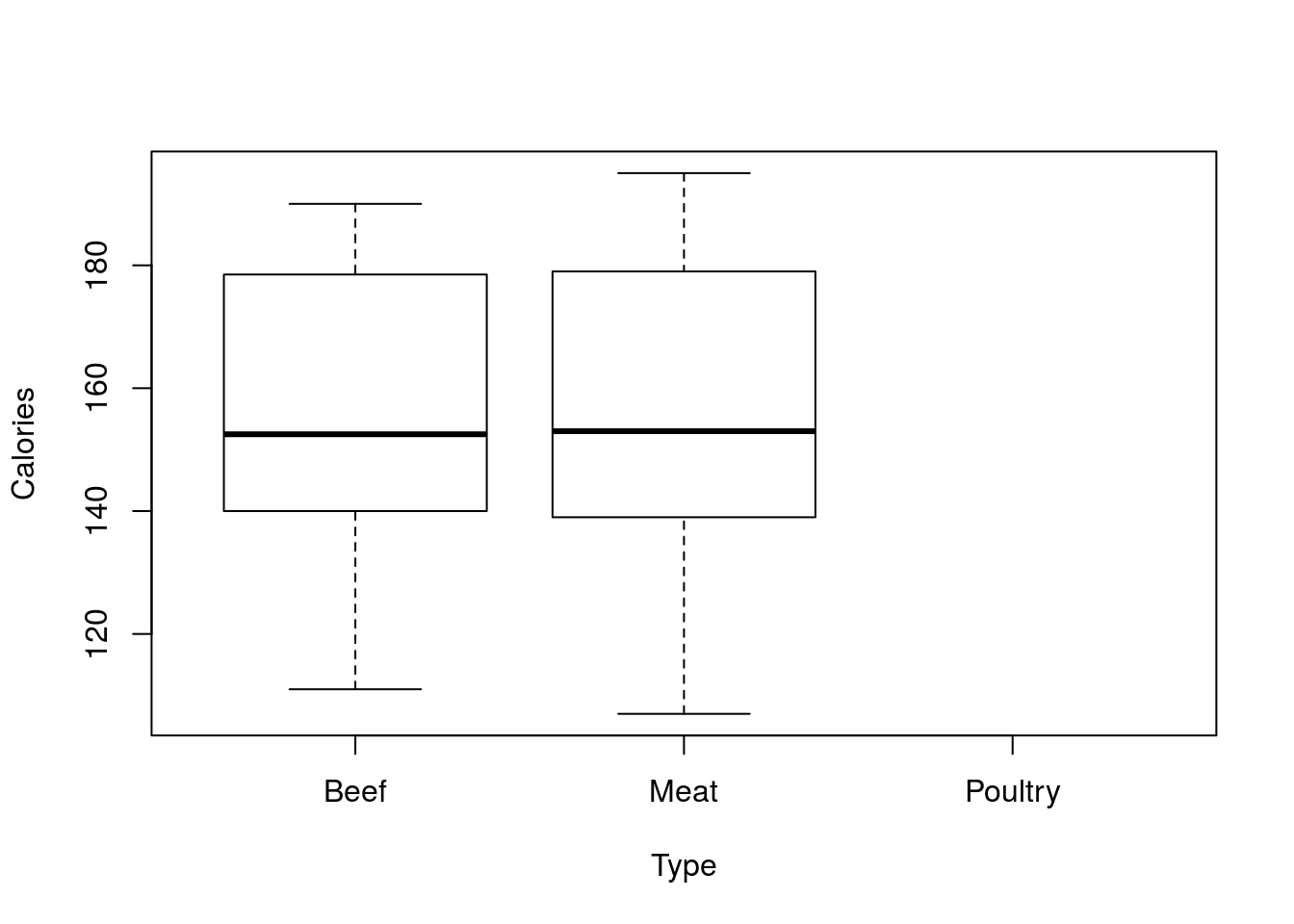
Now the bar for Poultry is gone[*] This can also be set with mfcol = (nr, nc) to similar effect. The difference is the order in which the plots are filled. Setting mfrow means that the plots will be made in rows, mfcol means they will be filled in columns. For our example, and most we use, this distinction won’t be important, and mfrow is slightly more often the intuitive choice. , and we only had to type it once. This approach also allows a number of other features in several functions we will be using later in the semester. Getting used to using the data = argument will make accessing those a lot simpler for you.
6.5.4 Histograms
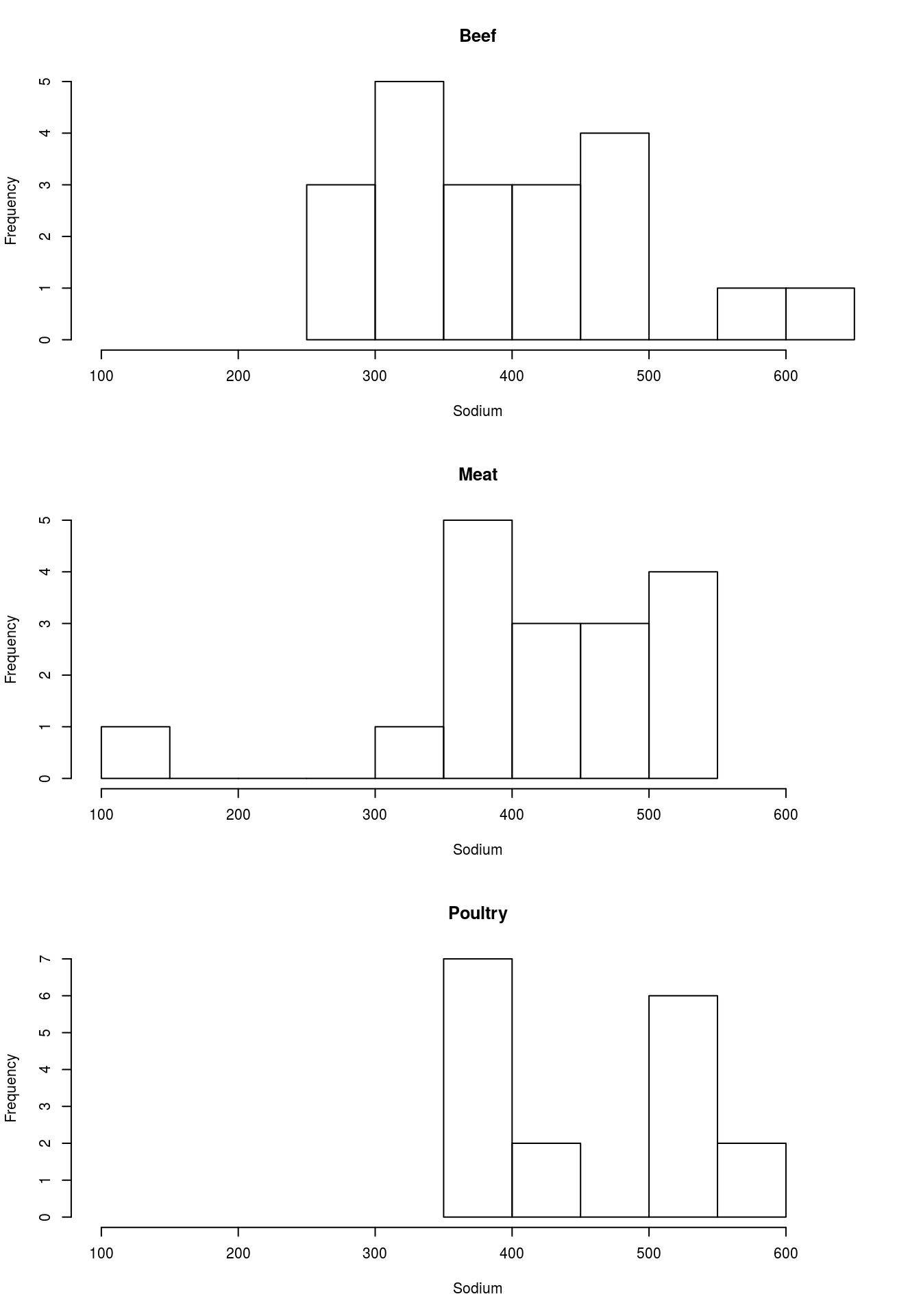
Unfortunately, there are no such easy tricks to make histograms from a single column. We will, instead, just have to set our parameters and use the [ ] selection to make each histogram individually. Here, let’s go ahead and put all three types in one plot.
# set the parameters
# NOTE using 3 instead of 2
par( mfrow = c(3,1))
# Make the histograms
hist(hotdogs$Calories[ hotdogs$Type == "Beef"])
hist(hotdogs$Calories[ hotdogs$Type == "Meat"])
hist(hotdogs$Calories[ hotdogs$Type == "Poultry"])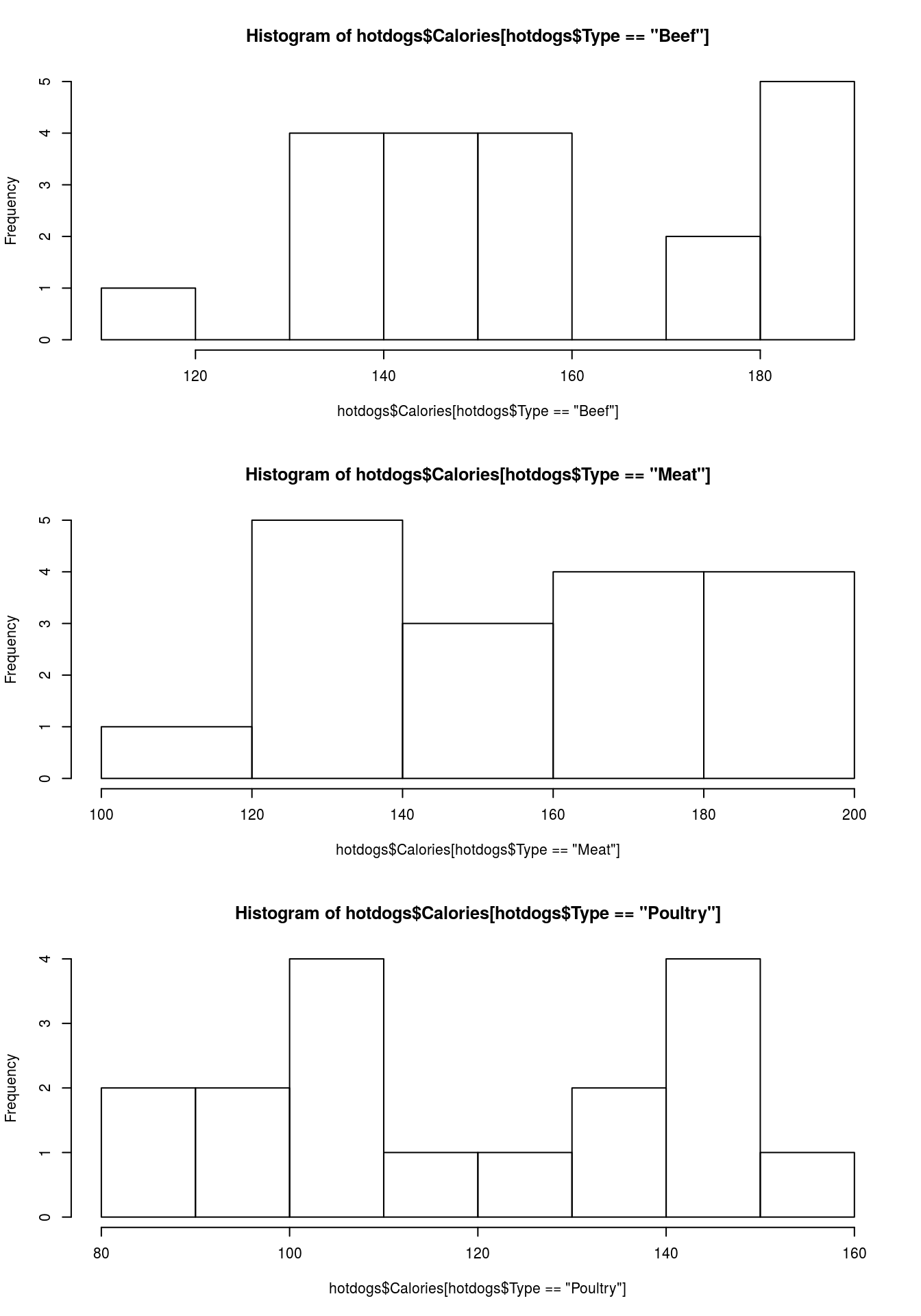
# Reset so we don't keep putting two plots on each thing.
par( mfrow = c(1,1))Note that the titles and axis labels are rather ugly, because of the long information we pased in. Add better labels and set the xlim to make all of them the same. You should get something like this:
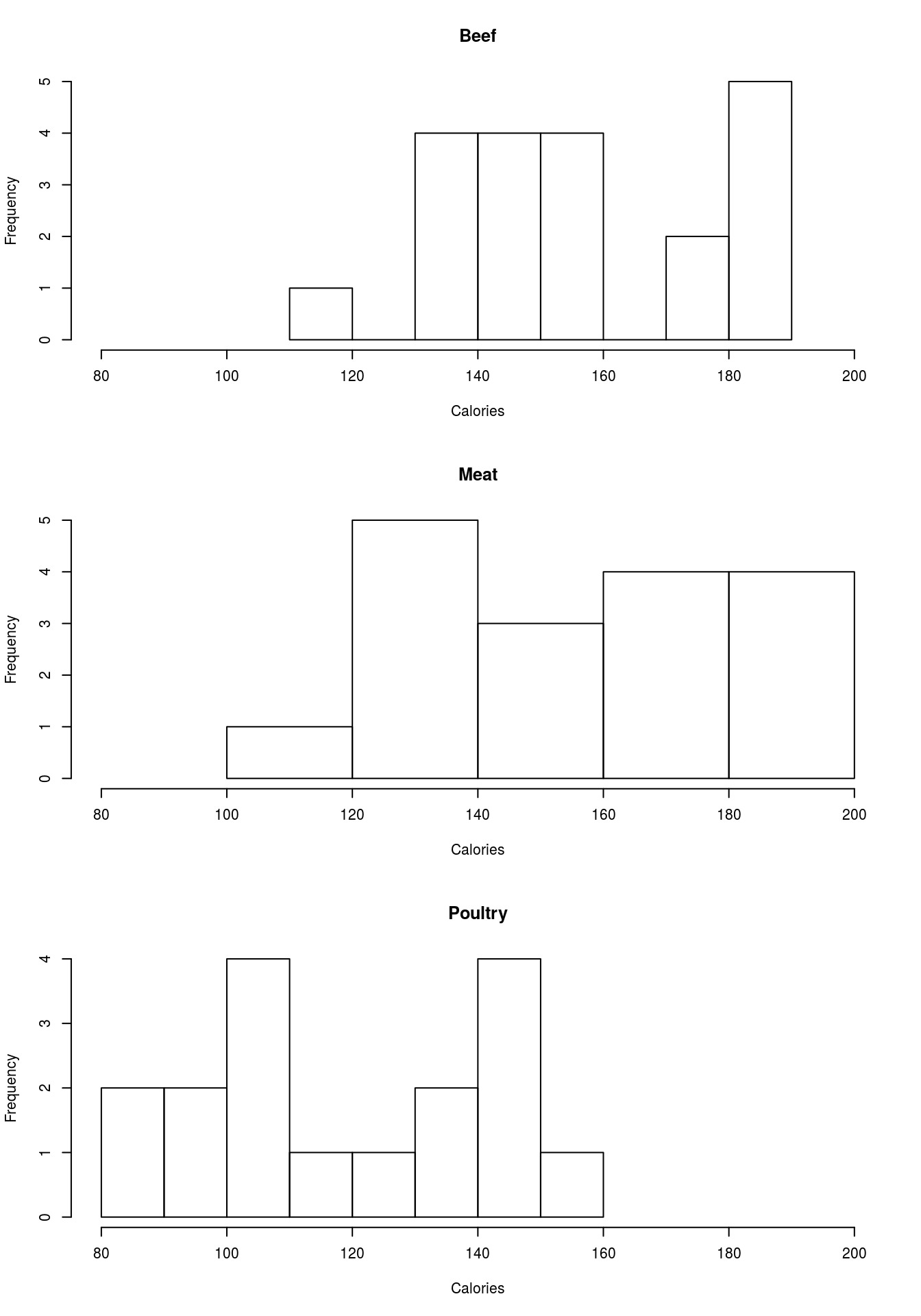
6.6 Try it out (II)
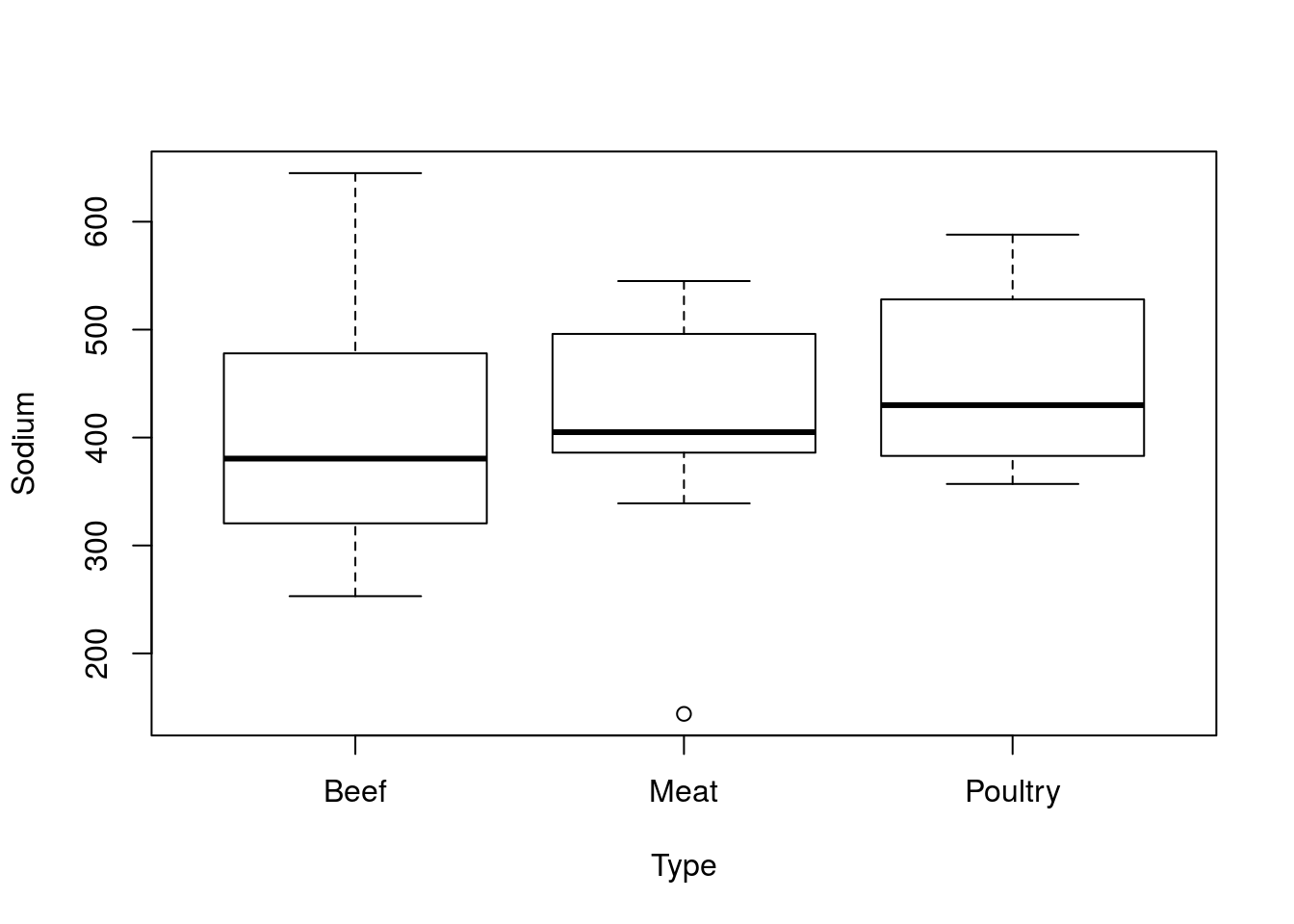
Try this out on your own by analyizing the differences in Sodium by Type. You should get outputs that look something like this.
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|
| Beef | 253 | 321.2 | 380.5 | 401.2 | 477.5 | 645 |
| Meat | 144 | 386.0 | 405.0 | 418.5 | 496.0 | 545 |
| Poultry | 357 | 383.0 | 430.0 | 459.0 | 528.0 | 588 |